Пожалуй, самой популярной и напрямую ассоциирующейся с казино игрой является рулетка. Попробуем разобраться, что это такое с математической точки зрения. Усаживайтесь поудобнее, рассказ обещает быть длинным и интересным.

Для начала нужно разобраться в правилах этой игры и немного покопаться в истории. С чего все началось, доподлинно неизвестно, история рулетки загадочна и содержит массу мифов. Одна из версий создания игры отсылает нас к Блезу Паскалю, который, пытаясь создать вечный двигатель, сначала сделал колесо, аналогичное современной рулетке, а затем даже нанес на него числа и стал кидать шарик, для предсказания выпадения номеров лото.

Современная рулетка появилась в конце XVII – начале XVIII веков и сразу обрела очень большую популярность. Ее много раз запрещали на государственном уровне, но это не прерывало ее сущестования, а лишь придавало запретного шарма. Сейчас существуют французская, она же европейская, и американская рулетки. Французскую можно встретить практически везде, кроме Соединенных Штатов, где мы найдем, соответственно, американскую. Принцип игры один, но имеется несколько важных различий.

Blaise Pascal

Попробуем разгадать секрет популярности рулетки и ответить на ключевой вопрос, можно ли в нее выигрывать с точки зрения математики.

Рулетка представляет собой колесо, на которое нанесены числа от 1 до 36 в черных и красных секторах, также имеются отдельные сектора зеленого цвета: с нулем – так называемое «зеро» и, в американской рулетке, с двумя нулями – «дабл зеро». Крупье запускает шарик над колесом в сторону, противоположную вращению рулетки, а каждый сектор имеет отдельное углубление, чтобы шарик мог остановиться на каком-то одном из них. Во время вращения шарика и рулетки игрок пытается предсказать, какое число выпадет. Существуют разные виды ставок: можно поставить на одно число, на несколько, или даже на треть или половину всех имеющихся чисел. От точности ставки зависит возможный выигрыш.

Интересно, что числа на колесо рулетки нанесены вовсе не в хаотичном порядке, как это может показаться на первый взгляд. Во-первых, последовательность чисел и цвет секторов для них всегда постоянны. Для европейской рулетки (с нуля и по часовой стрелке):

Для американской рулетки:

Во-вторых, в основе лежит система, способствующая наиболее случайному распределению чисел. Если разделить европейскую рулетку умозрительной линией напополам (от нуля до границы секторов 10 и 5), то на каждой половине колеса будут:

девять чисел каждой возможности из пар красное-черное, чет-нечет

шесть чисел каждой дюжины (1 – 12, 13 – 24, 25 – 36)

три числа каждой шестерки (1 – 6, 7 – 12, 13 – 18, 19 – 24, 25 – 30, 31 – 36)

сумма чисел на каждой половине равна 333

Для американской рулетки закономерности другие:

красные сектора напротив черных

после двух четных идут два нечетных

нечетные сектора напротив вышестоящих четных (например, 27 и 28)

Французское поле

Американское поле

На рисунке: слева американская рулетка, справа – французская.

И поля для ставок:

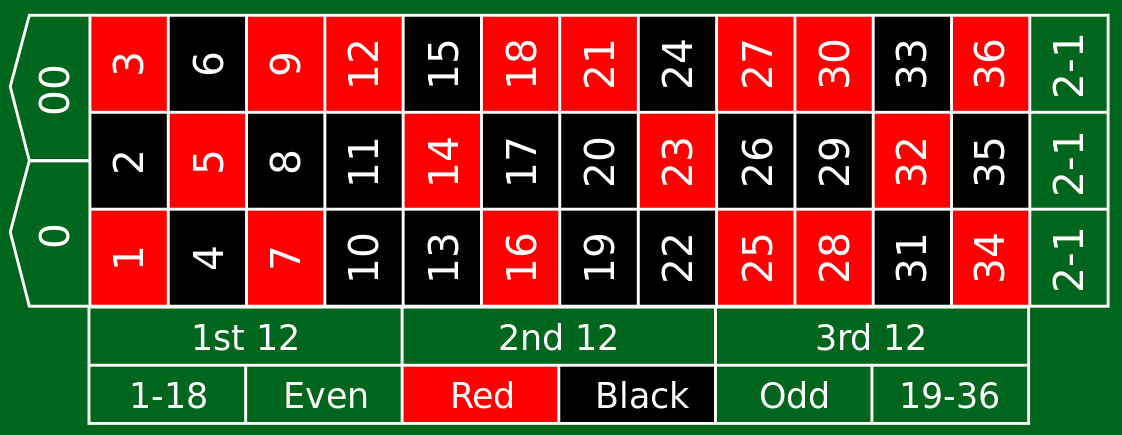
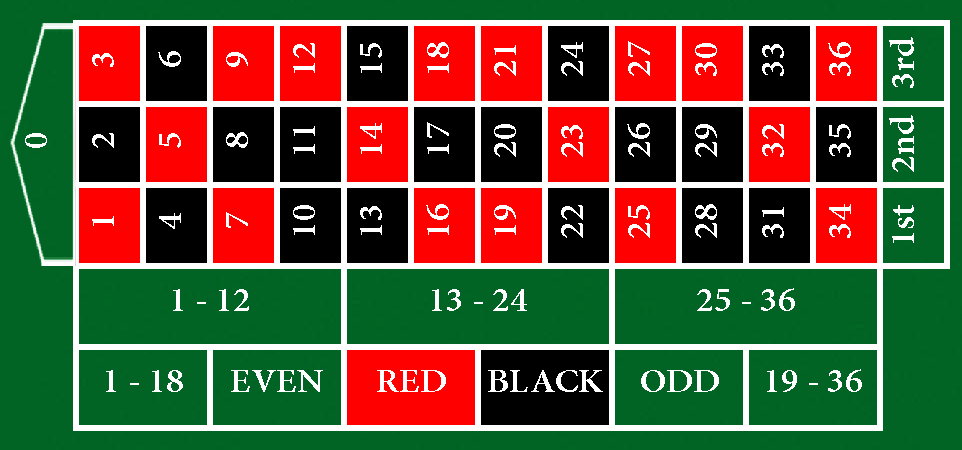
Все вышесказанное с точки зрения теории вероятностей говорит о том, что выпадающее в рулетке число является случайной величиной. Случайной величиной в теории вероятностей называют такую величину, которая в каждом испытании принимает только одно заранее непредсказуемое значение, зависящее от случайных факторов. Также случайными величинами являются четность, красное-черное, дюжина, в которую входит выпадающее число и так далее.

Это рождает много возможностей для разнообразных ставок. Можно поставить на 18 или на 12 чисел (красное-черное, чет-нечет, дюжины, колонки) – такие ставки будут называться внешними, также можно поставить на 6, 4, 3, 2 или одно число – такие ставки называются внутренними.

И, в-третьих, числа расставлены так, что ставка на сектора, расположенные рядом на колесе рулетки, максимально усложнена.

Далее мы подробно рассмотрим ставки и возможности для выигрыша во французскую рулетку, а также основное отличие рулетки американской.

Каждая случайная величина характеризуется набором значений, которые она может принимать, с соответствующими им вероятностями. Сумма вероятностей всех значений случайной величины равна 1, так как в испытании она обязательно примет одно из них. Кроме того, каждая случайная величина имеет некое средневероятное значение – математическое ожидание, которое равно сумме произведений всех возможных значений случайной величины на соответствующие вероятности.

Теперь перейдем к самому интересному – к возможному выигрышу. Дело в том, что это тоже случайная величина, математическое ожидание которой можно рассчитать. Более того, казино это математическое ожидание давно рассчитало, зафиксировало и, очевидно, в свою пользу. Внимательный, но азартный читатель возразит, что математическое ожидание ничего не говорит об исходе конкретного испытания, и будет прав. Действительно, в конкретном испытании можно угадать число и сорвать большой куш, хотя это событие исключительно маловероятно. Однако чем больше времени игрок проводит за игрой в рулетку, тем ближе его суммарный выигрыш к математическому ожиданию, так как в данном случае в дело вступает закон больших чисел. Он говорит о том, что среднее значение при увеличении количества испытаний стремится к математическому ожиданию. Именно поэтому полезно будет рассчитать математическое ожидание выигрыша.

Начнем с самых азартных ставок. Предположим, вы хотите поставить на одно число – 13 черное. Если вы угадаете, казино выплатит вам ставку в 35-кратном объеме. Здесь нужна небольшая оговорка. Вы получите вашу ставку, умноженную на 36, то есть при победе со ставкой в 1000 рублей, вам выплатят 36 000 рублей, однако ваш выигрыш будет равен только 35 000, так как необходимо вычесть из этой суммы вашу же 1000 рублей ставки.

Оно будет отрицательным! То есть чем больше времени проводим за игровым столом, тем ближе мы к проигрышу, а казино, в свою очередь, проводя тысячи и тысячи игр, имеет гарантированную прибыль в 2,7% от сделанных ставок.

Так почему же так получается: интернет полон «выигрышных стратегий», а на деле выходит, что математическое ожидание при любой ставке отрицательно.

Все дело в секторе «зеро». При любой нашей победе, казино расчитывает выигрыш без учета этого сектора, как будто чисел 36. Но их 37. Этот маленький перевес и дает казино постоянный доход в размере 2,7% от ставок. Какие бы вы не пытались применять стратегии, побеждать казино на регулярной основе у вас не получится. Все подобные игры придумали не для того, чтобы подарить вам денег, а наоборот, чтобы на вас заработать. А рапространение и даже реклама «выигрышных стратегий» только на руку казино.

Давайте разберем самую популярную из них – «Мартингейл».

Суть заключается в том, что вы ставите на «половину стола» и в случае проигрыша удваиваете ставку. Ставим на черное и, планируется, что в один прекрасный момент ваша ставка, наконец, сыграет и уж тогда-то вы все вернете и отыграетесь. Обычно приводятся следующие примеры:

Но давайте и тут применим нашу беспощадную математику. Во-первых, даже если предположить, что вы выиграли на ставке, скажем, 16 000, в вышеприведенном случае, то ваша выплата составит 32 000 рублей. Солидно. Но ведь вы поставили 16 000, да еще и до этого уже проиграли несколько ставок: 16000 + 1000 + 2000 + 4000 + 8000 = 31 000 рублей. То есть ваш выигрыш будет только 1000 рублей, но и для этого нужно было вложить 31 000. Но есть еще «во-вторых».

Вам может показаться, что если красное выпадает снова и снова, то это увеличивает шанс выпадения черного номера. Это распространенная ошибка. Результат каждого конкретного испытания не зависит от результатов предыдущих испытаний. Более того, если результаты того или иного испытания распределены, как нам кажется, равномерно, без длинных серий одинаковых результатов, есть причина подозревать подделку результатов. То есть серия красных номеров может продолжаться так долго, что либо у вас закончатся деньги, либо вы дойдете до верхнего ограничения ставки, которое установило казино, прекрасно осведомленное о существовании Мартингейла. А упереться в этот потолок, увеличивая ставку в геометрической прогрессии (каждый раз умножая на 2), очень легко.

Ну и, в-третьих, не стоит забывать о существовании сектора «зеро». Если выпадает «зеро», казино забирает все ставки на красное-черное.

Мы описали игру на французской рулетке, где получилось, что математическое ожидание выигрыша на стороне казино с величиной в 2,7%. А что же в американской?

Еще стоит рассказать о попытках игроков различными способами предсказать поведение шарика. В истории существовало несколько ярких примеров.

Joseph Jagger

Во второй половине XIX века британский инженер по имени Джозеф Джаггер предположил, что колесо рулетки не может вращаться идеально, и должны быть неточности в его работе. Он взял в помощники нескольких друзей, они начали ходить в конкретное казино в Монте-Карло и просто следили за игрой, записывали выпадающие числа, а затем анализировали полученные результаты. Их усилия были вознаграждены. На одном из столов обнаружились числа, выпадающие чаще остальных.

Таким образом в 1875 году Джозефу с друзьями удалось выиграть 60 тысяч фунтов (на современные деньги это примерно 6 миллионов долларов). После чего казино начало переставлять столы, а части колес менять местами так, что данная стратегия перестала работать. Данный случай был увековечен в книге Джека Лондона «Малыш видит сны».

Кадр из фильма «Короли рулетки»

У Джозефа Джаггера был и современный успешный последователь – испанец по имени Гонсало Гарсия-Пелайо был отцом многодетного семейства и по образованию математиком. Он задейстовал оба этих ресурса. В девяностых годах прошлого века пятеро его взрослых сыновей ходили по Мадридским казино и записывали результаты игр, а отец анализировал и искал подходящий для игры стол. Сколько им удалось выиграть нам не известно, но через какое-то время семейство Гарсия-Пелайо перестали пускать в Мадридские казино. Но они не остановились на достигнутом и перешли сначала на другие европейские казино, а затем и в столицу азартных игр – Лас-Вегас. Раз за разом им отказывали в посещении, а затем даже подали против отца семейства иск в американский суд. Судебное разбирательство длилось несколько лет, но в итоге Гонсало был опрадан, а его история увековечена в кино под названием «Короли рулетки».

Еще были как минимум две интересные попытки обыграть казино при помощи технических средств. В 1978 году два студента Калифорнийского университета пытались рассчитать сектор рулетки, куда приземлится шарик, при помощи ЭВМ, встроенных в их ботинки. Один из них при помощи большого пальца ноги вводил начальное положение шарика после прохождения им двух кругов, а второй получал ответ от компьютера, также на свою ногу, при помощи вибрации. Им удалось выиграть всего несколько тысяч долларов, но и их попытка увековечена в музее одного из казино в Лас-Вегасе. Еще одна группа физиков из Великобритании, уже совсем недавно, 2004 году, работала с приборами, спрятанными в их мобильные телефоны. Три человека распределили роли следующим образом: двое из них при помощи лазеров замеряли скорости движения шарика и рулетки, а третий получал расчет от удаленного компьютера себе на мобильник и делал ставки. У этой команды за несколько дней был неплохой результат – больше миллиона фунтов. Казино попыталось оспорить выигрыш, подало иск в Скотланд-Ярд, но суд встал на сторону игроков, так как они не влияли на положение шарика или движение колеса.

Подобные истории успеха выглядят привлекательно до тех пор, пока не взглянуть на них трезвым взглядом. Очевидно, что нельзя обыграть рулетку с помощью математики – математика всегда на стороне казино.

Все выигрывавшие крупные суммы выходили за пределы математической модели и искали ее недостатки (несовершенство колеса) или строили модель физическую (замеряя скорость шарика и колеса). Сегодня проделать подобное весьма непросто. Во-первых, любой сбор статистики в казино не приветствуется, а всем пытающимся могут просто отказать в посещении. Во-вторых, казино тщательно следят за состоянием рулеток, своевременно заменяют изнашивающиеся части, используют легкие пластиковые шарики и даже практически ежедневно меняют местами роторы рулеток для наибольшей равномерности износа.

В заключение скажем, что популярность данной игры понять несложно. Она проста в своем исполнении.

Попытался угадать число – через несколько секунд уже виден результат попытки. Плюс выигрыш, который нам обещает казино, может быть довольно существенным. Однако перед игрой лучше подумать. Тогда скорее всего, вас посетит очень простая, но очевидная любому, кто смыслит в математике, мысль: выиграть у казино можно, но выигрывать – нет. А если принять во внимание общий принцип игры, то получится, что вы пытаетесь обыграть не казино, не крупье, а теорию вероятностей, и победа здесь уже известно на чьей стороне.

Также позволим себе личную оценку и одобрим выбор известного персонажа в пользу карточных игр и сопровождения, так как в них вы играете хотя бы с человеком и получаете удовольствие от общения и соревнования.