
З
Золотое сечение
Такое деление единственно, и если принять за большую часть а, то из того, что
следует, что

Показываем.

Как именно это следует?



(ну или, если быть совсем точным – образы этих отображений),
Поскольку второй корень оказывается отрицательным, а мы рассекали отрезок, длина которого есть число положительное, то положительным числом должно быть и отношение его частей – поэтому выбираем положительный корень.
Таким образом, Золотое сечение – это число

Иррациональность Золотого сечения можно увидеть, и не решая квадратное уравнение. Помните, мы писали про непрерывные дроби и показывали, что любое рациональное число представимо в виде конечной непрерывной дроби?
И наоборот, если непрерывная дробь никогда не обрывается,
то число, которое представлено такой бесконечной непрерывной дробью, является иррациональным.
И наоборот, если непрерывная дробь никогда не обрывается,
то число, которое представлено такой бесконечной непрерывной дробью, является иррациональным.
Понятно, что мы здесь имеем ту же бесконечную рекурсию,
или самоподобие, которое возникало при попытке представить
в виде непрерывной дроби корень квадратный из 2 (См. здесь,
часть V. √2 и геометрический смысл алгоритма Евклида)
или самоподобие, которое возникало при попытке представить
в виде непрерывной дроби корень квадратный из 2 (См. здесь,
часть V. √2 и геометрический смысл алгоритма Евклида)
Но требуемое представление мы можем получить уже из равенства
Потому что, коли равенство выполняется, то мы
можем подставить выражение для x вместо знаменателя:
можем подставить выражение для x вместо знаменателя:
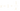

Иначе говоря, мы получили цикл, и, как следствие, представление Золотого сечения в виде бесконечной непрерывной дроби, а, значит, это число иррационально.





Есть вопросы по материалу?
Вы можете задать их в нашем специальном чате. Мы поможем разобраться в теме лучше
Понравилась статья?



